Technical Analysis

or How it Works and How it’s Done!

4.1) Introduction

After the Society announced that it was reducing the payments to With-Profits Annuitants (WPAs) by 20%, it was decided to collect data from annuitants to study the impact and try and identify any patterns. A computer model was developed initially to predict what the reduction might be, but later on to understand the likely future impact on annuitants’ pension payments.

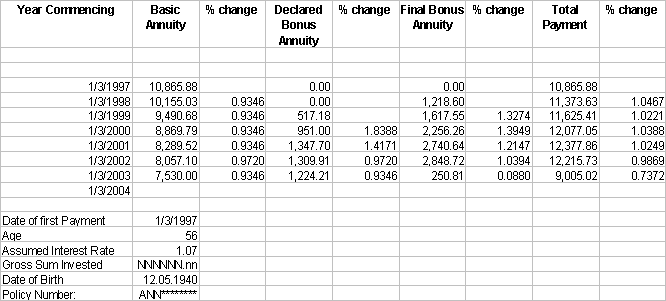
4.2) The Data.                 

Annuitants were asked to send the following details about their annuities: 

• Name (But we respect that some people may wish to remain anonymous
• Your Annuity number) (But we respect your wish not to supply this detail)
• Date of your first payment
• Your age at that time.
• Your assumed or anticipated bonus rate
• The gross sum invested
• Your Date of Birth
• The payments, including pence, for at least the last five years, preferably since the start of the annuity, taken from the annual statement, broken down as follows.
• Basic annuity
• Declared bonus annuity
• Final Bonus annuity
• Total gross annuity

4.3) The Equitable Life Annuity

The initial annuity is derived from the consideration money supplied by the annuitant and other factors such as gender, age, joint or single life, annuity rates in general, etc, etc. In the case of ELAS, there is a significant complication since the annuities being reviewed are called With-Profits Annuities. As one ELAS representative said, “Why would you want to take a Fixed Annuity, when you can take a With-Profits Annuity that will start at the same level as those offered by other Pension companies except that ours (ELAS’) will grow at least in line with inflation?”

The Equitable Life Assurance Society (ELAS) produces With-Profits Annuity - Annual Statements every year for each annuitant and which contain the following information:

The Renewal Date

Basic Guaranteed Annuity (BGA)

Declared Bonus Annuity (DBA)

Final Bonus Annuity (FBA)

Total Gross Annuity (TGA)

Historically, the Society also produced another document somewhat confusingly called the Bonus Declaration for the Year Ending 31 December 19NN, which contained references, amongst other things, to:

Anticipated Bonus Rate (ABR)

Overall Rate of Return (ORR)

Declared Bonus Rate (DBR)

N.B. In the footnote to each page is a summary of all the abbreviations used in each section as an aid to understanding.

So far as is known, the last Annual Statement that was issued is dated March 2000, announced the ORR and DBR for 1999, which became effective on 1^st April 2000 which, in the example illustrated, as the annuity started on 28^th of February, means that it became effective on 1^st March 2001. This is confusing enough, but the Society uses a concept known as the Interim Rate. In the year in question it was set at 9%, which the Society then used to compute the annuity payment, though the actual rate turned out to be 10%.

4.4) The Method

A model/simulation of the Society’s system was developed for analysing annuities initially to 'forecast' future results but subsequently was extended to evaluate:

a)      The consequences of decisions made by annuitants

b)      The strategy and tactics used by the Society to manage the With-Profits Annuities and their payments.

It is based, using M/soft Excel, on the detailed analysis of 72 annuity annuities supplied by 51 annuitants as evidently some have multiple concurrent annuities. These are linked to a summary page for statistical analysis and graphical output, which in turn is linked to a M/soft Word document. So far as can be judged, it is statistically valid though evidently the sample being self selected is not truly random in the accepted sense of the term. The data includes annuities from the late 80's through to 2000 and include all types, sizes, options, etc.

The average annuity on the database is £8,620 compared to a claimed average by the Society of approximately £6,000. There are 17 annuities with annual payments in excess of £10,000 p.a. but these have not been removed to see the effect of the change, as it is not believed it would be significant. In any event, as annuitants’ details have been added, the “average values” that have been derived from the data have not varied significantly so that it is reasonably certain that the analysis is based on a valid data sample.

In the absence of direct access to the Society’s computer systems and internal records, it is not known if this is the method used by the Society but since this model gives results that correspond to reality then it is:

1. Not important if the Society uses an alternative system.

2. Logical to accept that the model accurately reflects that used by the Society.

4.5) The Model

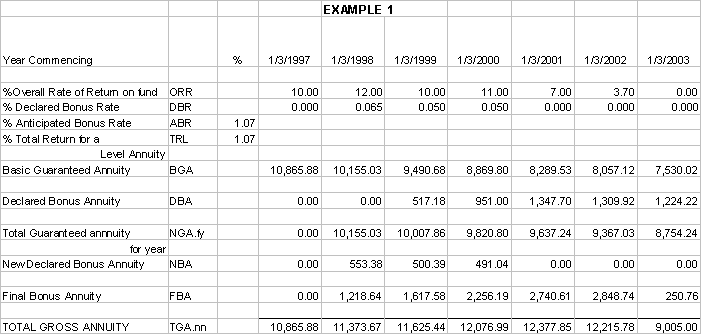
The data supplied by the annuitants, as illustrated above, is put into a second spreadsheet, as shown in EXAMPLE 1 below. There is one spreadsheet for each annuity and these are then summarised automatically for statistical analysis and generate the charts displayed in Section 2.

The model of the system used by the Society is in itself of interest as it throws up a number of points that are not immediately visible from the documentation given to annuitants. Regrettably in order to illustrate these points it is necessary to enter into some technical detail. However if there is to be any true understanding of the issues involved, the effort is essential

EXAMPLE 1 includes all the changes to the ORR, DBR & TRL made by the Society plus the various uplifts and reductions imposed by the Society in recent years.

As will be immediately obvious, in addition to the abbreviations mentioned earlier there are several others that must be added to the menagerie. These are as follows:

Total Guaranteed Annuity (NGA)

New Declared Bonus Annuity (NBA)

Total Return for a Level Annuity (TRL)

The last complexity is that in this section, some of these abbreviations will have some extensions such as:

 “.ly” for Last Year, “.ty” for this year or  “.01” for 2001, “.99” for 1999, etc

At the outset of the annuity, the annuitant transfers a sum of money, the consideration, in exchange for a regular payment, the annuity. The annuitant agrees with the Society in advance an Anticipated Bonus Rate (ABR).

Prior to 1997, the Society offered a facility called a GIR, Guaranteed Interest Rate, which was set at 3.5% above the anticipated rate of return. There may have been other rates but annuitants have not sent any. The TRL for GIR annuities is the ABR * 1.035. The TRL for non-GIR annuities is the same as the ABR. EXAMPLE 1 illustrates a non-GIR annuity.

For the reasons explained below and which relate to how the Society computes the TGA, the model does not precisely calculate the value of the TGA. The difference is not large, between ½ and 1%, is NOT cumulative and is ONLY significant when the model comes to forecast the exact reduction of an annuitant’s annuity before their renewal date. A request for a detailed explanation has been sent to the Society but there has been no response so far.

Subject only to the difference above, the model computes exactly all the values of the BGA, DBA, FBA & TGA for all years from three basic sets of data:

1. The initial annuity payment

2. The Anticipated Bonus Rate (ABR)

3. The start date of the annuity.

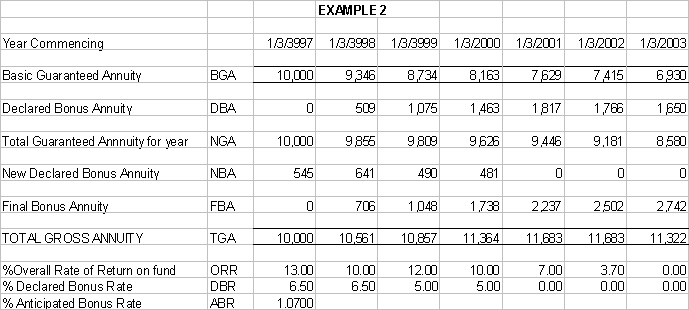
Self evidently, the model also uses the various bonus rates issued by the Society, as described above, but they apply to all annuitants though they are different for GIR and non GIR annuities.

In EXAMPLE 2 the starting Guaranteed Basic Annuity has been rounded for purposes of clarity and will be used as the basis for illustration in this section.

The actual calculations may be a little esoteric but there are two reasons why the underlying logic may be worth absorbing:

a)      Many annuitants have stated they do not understand how their annuities are calculated and they would like to know, as is surely their right.

b)      Understanding the Society’s calculations, will lead to a better understanding of what the Society is doing or not doing on behalf of its members, the WPAs.

A) The Basic Guaranteed Annuity (BGA) is computed as follows, after the first year:

BGA.ty  = BGA.ly / ABR          or         9,346 = 10,000 / 1.07

This is repeated each year, so that the BGA always declines at a constant rate, save in the most exceptional circumstances as in 2002 described below. Any variation must be approved by a majority of members and by the Court. Any further variation in BGA or DBA seems very unlikely.

B) The Declared Bonus Annuity (DBA) is computed as follows:

a)      In the first year, the New Declared Bonus Annuity (NBA) is derived first as follows:

BGA.ty x DBR x No of days between the start date and year end / 365 (In the example, the start date was 28^th February)          or         10,000 x 0.065 x 306 / 365 = 545

This value is not added to this year’s annuity but carried forward to the second year.

The DBA for the first year is always zero.

Most annuitants do not know that the start date of the annuity is not the date of the first payment, but appears to be the date when the annuity was processed, which is not necessarily the same The start date of the annuity in theory can be easily derived by backwards iteration and most times is easily computed but in practice turns out to be another source of error. For a small percentage of annuities, the value for the initial DBA is not immediately computable by this method and which leads to the conclusion that the data was entered into the system incorrectly as no other explanation seems logical. This has no long-term significance partly as the difference is only a few pennies and the method used by the Society is to some extent self correcting, since any error here is compensated by the way Final Bonus Annuity is calculated.

b)      In the second year, the Declared Bonus Annuity is computed as follows:

DBA.ty  = DBA.ly + NBA.ly / ABR                  or         (0 + 545) / 1.07 = 509

NBA.ty is computed as follows in two steps:

i) NGA.ty  = BGA.ty + DBA.ty or         (9,346 + 509) = 9,855

ii) NBA.ty  = NGA.ty x DBR.ty or         (9,855 x 0.065) = 641

This step is then repeated for each year in succession.

In the 2002, the Society increased the GBA and DBA by 4% for all annuitants (0.5% for GIR’s) as part of the Compromise Deal and that calculation is as follows:

BGA.ty = BGA.ly / ABR x 1.04             or         7,629 / 1.07 x 1.04 = 7,415

DBA.ty = DBA.ly / DBR.ty x 1.04        or         1,817 /1.07 x 1.04 = 1,766

There is one other feature of the DBA that must be mentioned. In EXAMPLE 2, the DBR for 1997 has been set at 6.50%, mainly to illustrate the basis of the calculation. In the process of analysing all the data, it was obvious that certain annuitants, where the start date of their annuity lies between January 1^st and March 30^th were not treated the same way as other annuities. In the first year their DBR was always set to zero. The Society states that this is because in that period, just as with the ORR, the DBR cannot be known and rather than use the previous year’s DBR, surely the most logical thing to do, it decided to set it at zero.

Now it is important to be clear that this has no effect on the Total Gross Annuity, at least not until the 20% reduction is applied, (See below) but it does have the effect of reducing the DBA, which is guaranteed, and increasing the FBA, which is not guaranteed and thus can be removed by the Society. The significance is that, using EXAMPLE 1, after the 20% reduction had been applied, the TGA in 2003 would have been approximately £300 higher that that actually paid.

C) The Final Bonus Annuity (FBA) is computed as follows:

FBA = TGA – NGA                 or         11,683 – 9,181 = 2,502 (2002)

This is the normal calculation, but in 2003 the Society introduced a 20% reduction to the Final Bonus Annuity. (FBA) For many annuitants the above calculation would have meant the FBA would have become negative, which is obviously not permissible because it would break the contractual terms of the annuities. Under these conditions the FBA is computed as follows:

IF TGA.03 – NGA.03 is greater than zero,                     THEN FBA.03 = TGA.03 –NGA.03

IF TGA.03 – NGA.03 is less than or equal to zero,          THEN FBA.03 = 0

Actually, since this results in an unequal reduction for different annuities and annuitants, it would have been more logical to permit the FBA to go negative so that all annuitants received the same percentage reduction on their TGA. However, as stated above, this would have been a breach of contract.

D) The Total Gross Annuity is the most contentious of all the elements that go to make up the annuity for the WPAs – not least since how this is calculated directly affects how much the annuitant receives. As noted above, the formula has never been explained in any detail and even where it has the results of the formula do not appear to work. What is known is that the Society decided that, as it could not know the true ORR in the early part of the year, it would use a so called Interim rate for the first part of the year and after April 1^st the ORR as announced by the Society.

It is not appropriate to comment on this issue in this section other than to say, there are easier ways that deliver results that very closely match those derived by the Society and it is those that will be described.

The model uses this simplified version, which produces perfectly adequate values for the purposes of this analysis and is as follows:

TGA.ty = TGA.ly / TRL x ORR            or         10,857 = 10,561 / 1.07 x 1.10

As noted above, in 2003, the Society introduced a 20% reduction that was imposed on all WPAs. The computational logic of the Total Gross Annuity and the FBA in 2003, which was a little more complex, is as follows:

If (TGA.03 -TGA.02 *0.2)         is less than TGA.fy,

Then TGA.03 = TGA.fy            and       FBA = 0

Else TGA.03 = TGA.03- TGA.02 *0.2   and       FBA = TGA.03 - TGA.03

Or 11,448 - (12,216 * 0.2) = 9,005 which is greater than 8,754 so

TGA.03 = 9,005 and FBA = 9,005-8,754 or 251

There is no pretence that the formula described above gives an exact duplication of the FBA, although the difference is relatively small, typically less than 0.5% or approximately £500 in an annuity of £10,000 p.a. The model continuously adjusts for the error so that the overall results remain in line with the numbers given by the annuitants. The key point is that the underlying logic of the process by which the Society derives the annuities is not obscured and it is that issue that is being explored.

In recent years there have been other alterations as follows:

1.       Following the House of Lords ruling the ORR was reduced by 1% in 2001 and 2002 and by 1.5% in 2003 and 2004.

2.       As part of the Compromise deal the TGA was increased by 2.5% in 2002.

These changes come into force on the anniversary of the annuity though they are not based on a calendar year, but on the Society’s year, which appears to run from April to March.

4.6) General Rules about the ELAS With-Profits Annuities

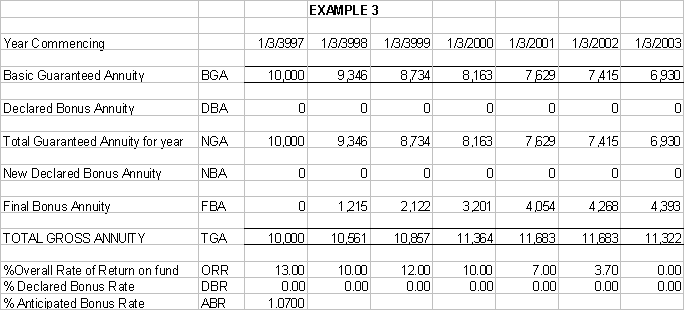
As a result of the analysis, it appears that the following logic applies to all With-Profits Annuities with Equitable Life Assurance Society:

A) Overall Rate of Return (ORR) in relation to the Total Return for a Level Annuity (TRL)

Note:   For GIR’s,                    the TRL is the ABR increased by a factor of 1.035

          For non-GIR’s,              the TRL is the ABR and is NOT increased

B) Anticipated Bonus Rate (ABR) in relation to the Declared Bonus Rate (DBR)

If the ABR = DBR        then the                        NGA is             Level

If the ABR > DBR        then the                        NGA                Decreases

If the ABR < DBR        then the                        NGA                Increases

Note: In all conditions, the relationship between the ABR and DBR has no effect on the TGA and FBA

This logic is normally obscured since the ORR & DBR change each year and is ONLY evident when the values are set at a constant level over a period of time that the validity of these logic statements become clear.

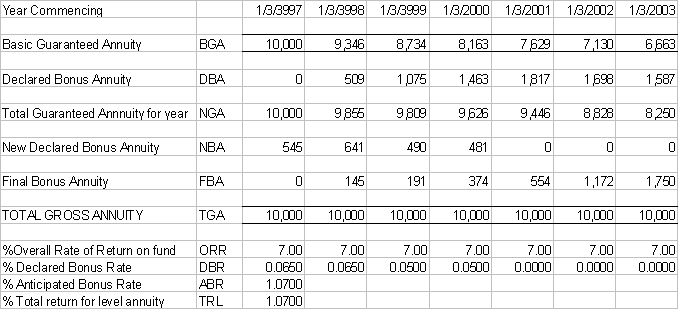
In EXAMPLE 3 below, with the same starting point, but setting the Declared Bonus Rate at zero, there is no change to the Total Gross Annuity, though as the Declared Bonus Annuity is now zero the Final Bonus Annuity increases to compensate.

This illustrates two very important points:

a)      The values of the BGA and DBA combined are independent of the value of the Total Gross Annuity.

b)      The Final Bonus Annuity is simply the difference between the two values

Thus there are two independent series, one, which determines the values of the BGA and DBA and the other, which determines the TGA.

It may not be obvious, but in order to achieve the same level of growth for a GIR annuity that a non-GIR annuity achieved, that is the TGA in 2003 would be £11,322, the TRL would be 11.0745 (10.7 *1.035), the ORR would need to be in excess of 13% each and every year! That is not possible in today’s economic reality, which may be an explanation of why the GIR annuity was withdrawn in 1996.

In addition, the model has identified some anomalies between what is normal and/ or what was stated or implied by ELAS in its documentation. In some cases this appears to be arithmetic errors on behalf of the Society, which implies that there is clerical intervention in the calculations of annuities. Quite why there should be these errors in what one would assume to be a highly automated, system driven methodology is not immediately obvious.

4.7) Life Expectancy

One of the consequences of the actions of the Society has been to remove a substantial amount of money from the WPAs for the remainder of their lives. For example, if an annuity is reduced by £3,000 p.a., the annuitant has not just had a reduction of £3,000 but £3,000 p.a. for the rest of his or her life. A new base level has been set, so that even if the annuity increases in the future it is from the new lower level. If the annuitant lived another 17 years, then whatever happens in the future, the annuitant has lost £51,000 income.

It follows therefore that one of the key numbers is how to determine the life expectancy of the ‘typical’ annuitant. The method chosen is to compute the number of years between the annuitants’ age at July 30^th, 2003 and the remaining ‘actuarial’ life expectancy of the annuitant.

Determining the life expectancy of the Society’s annuitants is a very specialised area of research and statistical study and lies outside the area of this analysis but the following has been extracted from various sources on the Internet and which are pertinent to this report.

a)      There is a BBC document that reports increasing life expectancy up by 5 years for men and 4 for women in the period 1980 to 2000. Thus it follows that by today, life expectancy has increased again.

b)       Life expectancy was 75.2 for men and 80.1 for women in 1999.

(Extracted from www.sustainable-development.gov.uk/indicators/regional/2001/h6.htm  and posted on the Internet, retrieved by a search using Google and “Life Expectancy” ) 

c)      Life expectancy is heavily weighted in favour of the social classes I, II & IIIN, the classes most likely to buy private pension funds. In 1996, the life expectancy for these classes is approximately 75.8 for men and 81.1 for women compared to the average across all classes of 73.9 and 79.3 respectively.

(Extracted from www.bris.ac.uk/poverty/wales/NHS-RAR_1.pdf and posted on the Internet, retrieved by a search using Google and “Life Expectancy”)

This implies the following that in 1999 the life expectancy for these social classes will be

75.2 / 73.9 * 75.8 = 77.1 for men

80.1 / 79.3 * 81.1 = 81.9 for women

Life expectancy is increasing steadily so that by 2003 it would be reasonable to expect a life expectancy of 78.6 for men and 83.5 for women. The actuarial age of death of 80 was selected as being a reasonable median age for the purposes of the model and this report.

It is worth noting that if the life expectancy is reduced by 1 year, the percentage reduction in the amount of money removed by the Society is approximately 1.25% p.a. In other words, even if the selected age of 80 is overly optimistic, the effect on the reduction over the lifetime of the WPAs is quite inconsequential!

4.8) Summary

The method used by the Society to compute the annuities is very subtle and as the variables vary each year more or less independently of each other, it is not possible to see what the effect of each change might be unless each variable is isolated from the others. This section has been devoted to an attempt to explain how each variable works.

1.       It is clear that the relationship between the ABR and DBR determines which part of and how much of the annuity, is in the terms of the Society guaranteed.

2.       It is clear that the relationship between the ORR and TRL determines the overall size of the annuity.  

3.       The difference between these two arithmetic series defines the TGA. It is this part of the annuity that is completely un-guaranteed by the Society.

The critical decision therefore is to choose the Anticipated Bonus Rate (ABR) that in the annuitant’s judgement best suits his or her needs. However: 

1. It is in the Society’s interests to take actions to maximise the size of the Final Bonus Annuity (FBA) since that gives it the maximum amount of “annuity” that can be withdrawn from future payments.

2. It is in the Annuitants’ interest to have the DBA as large as is possible since that element of the annuity in conjunction with the Basic Guaranteed Annuity that is guaranteed and cannot be removed.

These two objectives are in mutual contradiction.

In the other sections, how these inter-relationships work in real life, will be explored and various contentious issues exposed.

Note: The data sample is small and not truly random and the numbers and values used in the preparation this report are based on the data supplied by annuitants. It is possible that there are statistical anomalies or errors that have not been detected and that may result in some of the numbers used in this report being less accurate than they otherwise might have been. However, it is very unlikely that the conclusions, deductions and inferences that have been made have been materially affected by any such errors.

DOCUMENT A

Your with-profits annuity - planned reduction to income payments

Dear Mr Surname

1 am very sorry to let you know that we will need to make changes to your with-profits annuity, which will significantly reduce your income payments.  This letter gives you some warning, before your next review date.

We have done our best to protect you, as far as possible, from the major setbacks we have recently experienced.  However, unfortunately, to be fair to all our other policyholders, we must now begin to make these changes.

Reductions which have taken place so far on with-profits annuities

Since 20 July 2000, our decisions on bonuses have been particularly affected by:

• the failing value of investments in stocks and shares;
• the cost of guaranteed annuity rates (GARs); and

·         increases in the money we set aside for potential claims for compensation.

Following the House of Lords' decision in July 2000, we had to reduce the value of with-profits annuities.  We did this, other than for with-profits annuities, by reducing the policy value by 5% at that time.  We made significant further reductions in July 2001, April 2002 and July 2002.  This means, allowing for bonuses, our other with-profits policyholders have suffered an overall reduction of about 20%.

So far we have largely protected you from these falls. In fact, you and other with-profits annuitants have generally received a positive investment return of about 14% over the same period.

As we have said, most other with-profits policyholders have suffered significant reductions in the value of their annuities, whereas those who have with-profits annuities have not.  We were able to do this because if you have a with-profits annuity, you cannot withdraw your funds.  It was possible for us to phase the cuts to with-profits annuities in the hope of improved financial conditions.  Unfortunately, because conditions have not improved we can no longer keep doing this.

This basically means that with-profits annuities, like yours, are now out of line by about 30%.

Action we need to take now

We now need to bring with-profits annuities back into fine with other policyholders and we plan to do this over two years.  We will be putting in place the following changes.

• On your policy anniversary after 1 February 2003, we will reduce the value of your total annuity, which we would otherwise pay, by up to 20%.  This action replaces the current approach of reducing the overall rate of return over the term of the policy.  We will then reduce your income payment again in 2004 to regain any overpayment which may still apply.

• The interim rate of return for 2002 for all with-profits policyholders, except those with annuities, is zero.  From 1 December 2002 we will bring the interim rate of return for you into line, and this will also be zero.

• So far, we have only taken from with-profits annuity policies in force on 20 July 2000 (the date of the House of Lords' decision) part of the 5% reduction.  We have previously announced that we will recover this cost at the rate of 1 % each year for five years.  This adjustment applied in 2000 and 2001 and we will now recover the rest at a rate of 1.5% in 2002 and 2003, or as soon as bonus rates allow.

We also review the amount of your income payments each year at the anniversary of the date your with-profits annuity policy started.  That review reflects the gap between the expected bonus rate you chose and the bonus rate which applies.  This then sets the level of income payments you will receive for the following year.  The reductions quoted above will apply to the amount of annuity after this review.

We would like to emphasise that you will not receive less than the guaranteed payments under the annuity (known as the 'basic annuity' and 'declared bonus annuity') and this may reduce the effect of these reductions.

We have enclosed:

• a leaflet that includes details of how your with-profits annuity policy works;
• some examples of the effect of these changes; and
• other questions and answers you may find useful.

Why do we need to change now?

We originally decided to spread the reductions over the term of with-profits annuity policies because we hoped that poor investment conditions would recover reasonably quickly.  However, we are now in one of the longest periods of poor stock-market performance for many years.  And, like most other companies, we have suffered heavy investment losses.  We have reduced our investments in stocks and shares to very low levels in order to secure and stabilise the With-Profits fund. Unfortunately, because of our circumstances now - highlighted in the Interim Report that you should have received - we can no longer afford to phase these reductions in.

Summary

I am very sorry that we have had to take this decision.  We carried out a great deal of work to look for alternatives that would avoid reducing incomes in this way.  We had hoped to continue to reduce your income in a phased way over the term of your annuity.  However, our changing circumstances and the growing gap between with-profits annuities and other policies meant that it would have been very unfair to other policyholders to continue to act in this way.  We must balance the interests of all continuing policyholders and it is no longer fair to delay the reduction in values that our other policyholders have recently suffered.

Because we cannot set final bonuses in advance, it is not possible to provide individual calculations before the anniversary date.  However, 1 hope that the details set out above, together with the enclosures with this letter, will give you a reasonably clear idea of how much the reduction in your income next year will be.  You will, of course, receive a statement at your anniversary date in the usual way.

Yours sincerely

Charles Thomson

Chief Executive

(This is an undated document but received early November 2002, with the reference number 02/00000427/8926A/10v1. Copyright is acknowledged.)

1 Can you give me an idea of how my income payment will be affected by the final bonus rates announced?

Unfortunately, we cannot give precise percentages of the levels of reduction in income before the change comes into force because:

·         current bonus rates are not guaranteed in future; and

·         there is a wide range of policies available.

However, we have produced some examples in the table opposite, which we hope will help you.

To use the table opposite you need to know the date your policy started and also the anticipated bonus rate (ABR) you chose when you took your policy out.  You can find both of these in your original policy documents.

Find your start date in the first column and then look for the ABR that is equal to or is closest to the ABR, which applies to your policy.  Then run along the row for the start date and down the column for the ABR.  The percentage range is a guide to the approximate reduction to your gross income, which will apply from the first policy anniversary on or after 1 February 2003.

For example, Mr Smith began his policy on 15 April 1997 with an ABR of 4.5% (please see shaded box).  His current annual gross annuity is £4800, which means he receives a gross income of £400 on the first of each month.  On 1 May 2003, the first payment date after the next policy anniversary, we will reduce his income by between 21% and 25%.  This would mean his new monthly gross income would be between £316 (£400 less 21 %) and £300 (£400 less 25%).

Approximate reduction to gross incomes
Start date of policy	Anticipated bonus rate (ABR)
	2.5%	4.5%	6.5%
1 January 1987 to 31 December 1994	22% to 26%	24% to 28%	25% to 29%
1 January 1995 to 30 June 1996	21% to 26%	22% to 28%	N/A
	Anticipated bonus rate (ABR)
	4.5%	6%	7.5%
1 July 1996 to 31 December 1997	21% to 25%	22% to 26%	23% to 27%
1 January 1998 to 31 December 1998	17% to 21%	18% to 22%	N/A-
1 January 1999 to 31 December 1999	12% to 19%	13% to 20%	N/A
1 January 2000 to 19 July 2000	11% to 13%	12% to 14%	N/A
20 July 2000 to 31 December 2000	7% to 13%	8% to 14%	N/A

Notes:

1 The anticipated bonus rate is the rate you chose before the annuity started. We describe this reduction in your policy document.

2 We will always pay, at least, the guaranteed benefits under the policy (the basic and declared bonus annuity).  For that reason, the reductions shown in the table for policies, which began in 2000 are significantly lower than the changes shown for earlier policies.

3 The reductions shown are not the largest or smallest which could arise as the range depends on future bonus rates.

4 N/A stands for not applicable or does not apply.